きのこる庭

構文解析をしていてちょっと詰まったのでメモ。

上記の構文規則に基づくとすると、
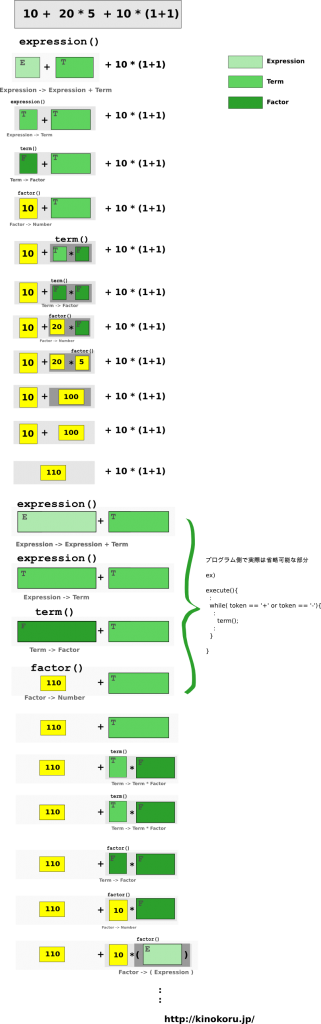
10 + 20 * 5 + 10 * (1 + 1)
の再帰ルーチンは以下のようになる。
(なお、 expression(), term(), factor() はそれぞれ上記の構文規則を実装した関数 )

簡単な解説

再帰的下向き構文解析って？

コンパイラとかで構文を解析する時に使う方法の一つ。

例えば以下の図は再帰的下向き構文解析を行うための簡単な規則の例です。

ここで使用しているそれぞれのワードについては以下の式を考えると分かりやすいかもしれないです。

10y + 3/5(10 + 10)

数学では 10y とか 3/5 とかのことを「項(term)」と呼ぶけど、
10y, 3/5 というのは
複数の変数・数値を割って成り立っているものなので、

10y = 10 * y
3/5 = 3 / 5 * (10 + 10)

というように、
項は 複数個の 割り算 または かけ算 によって成り立つ一つの単位として考えられるので、上記のような構文規則になります。

この項を足したり引いたりしたものをここでは「式(expression)」と呼びます。

10y + 3/5(10 + 10) は式です。

「あれ？そうすると ( 10 + 10 ) は式じゃないの？」
となりますが、こちらの 10 + 10 も立派な式です。
ですが、最初の expression() の段階では計算しません。
項を更に分割した単位である「因子(factor)」まで分解して 因子にたどり着いた段階ではじめて 式に変換して計算を開始します。

因子については、上の式で言うと

10, y, 3, 5, (10 + 10) にあたります。

10, y, 3, 5 はそれ以上分解できない「定数」「識別子」としてそのまま処理され、
括弧がついている場合は「その中に式がある」と判断して計算を開始します。