きのこる庭

　なんとなく機械学習周りのツールをいじってみて、いざ学習モデルを組んでみようとTensorFlowのコードを見てみた所、なにやら奇妙で膨大な処理がつらつらと書き連ねられていて圧倒された…なんて経験をされた方も少なくないと思われます。確かにTensorFlowのコードは一見すると複雑怪奇ですが、プログラムの背景に存在している以下の4つの概念を抑えてしまえば 膨大なコードもうまく紐解いてゆくことが可能です。

　この記事ではTensorFlowによる学習のコードを見て どこでどういう処理が行われているのかなんとなくイメージできる事を目標として、簡単なモデルの例からTensorFlowにおける学習の導入まで段階的に議論を進めていきます。

モデル

　TensorFlowでモデル構築…といえばよくある多層パーセプトロンがパッと頭に思い浮かびそうですが、TensorFlowで構築できるモデルは何もニューラルネットに限ったものではありません。例えば以下のコードを見てみましょう。

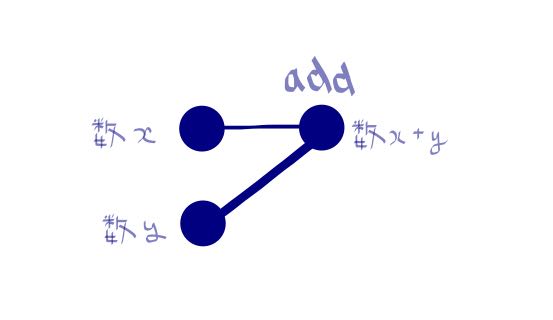
# -*- coding: utf-8 -*-
import tensorflow as tf

x = tf.placeholder(dtype=tf.float32)
y = tf.placeholder(dtype=tf.float32)
addition = tf.add(x, y)

　このコードを図で表すと以下のようなグラフ構造になります。

　この addition は「二つの数を足し算する」という単純なものですが、これも立派なモデルと言えます。ここで重要な事として、このモデル自体は「学習」や「実行」の意味合いを持ちません。実際の所、具体的にどのような2つの数を足し算するかも定められていませんし、ただ「二つの数を足し算する」という事を表しているだけです。このことに注目すると、TensorFlow関連の書籍でモデル構築をする際によく出てくる以下のようなコード(以下は単純な多層パーセプトロンの例)がどういうものか、何となく分かってきますね。

x1 = tf.placeholder(dtype=tf.float32) # 入力層
w1 = tf.Variable(dtype=tf.float32)
b1 = tf.Variable(dtype=tf.float32)
h = tf.nn.relu(tf.add(tf.matmul(x1, w1), b1)) # 隠れ層

w2 = tf.Variable(dtype=tf.float32)
b2 = tf.Variable(dtype=tf.float32)
y = tf.nn.softmax(tf.add(tf.matmul(h, w2), b2)) # 出力層

　隠れ層の部分を見てみましょう。これを言葉にすると「x1とw1を掛け合わせたものにb1を足し算したものを ReLUという関数で変換する」というグラフ構造です。これをhとして、今度は出力層を見てみましょう。出力層では、「hとw2を掛け合わせたものにb2を足し算したものを softmaxという関数で変換する」というグラフ構造になります。この y をモデルとして採用したものがいわゆる多層パーセプトロンです。

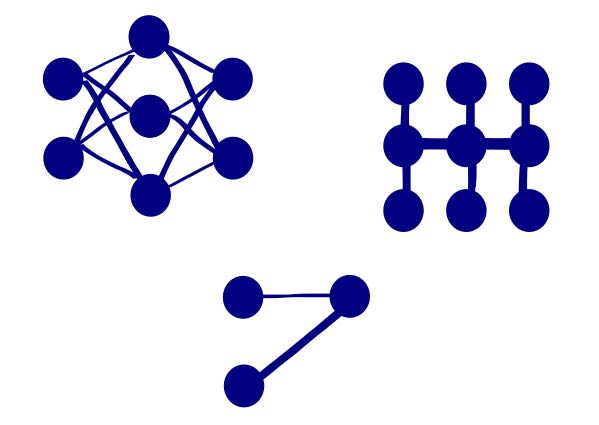
　このように、様々な計算を処理するための雛形となるものがモデルです。以下は様々なモデルのイメージです。このようにTensorFlowではグラフ構造に基づく柔軟なモデル構築が可能です。

モデルを用いた計算

　一旦先ほど定義した単純なモデルである addition の例に戻りましょう。モデルを構築した所で、今度は実際に何かしらの入力を加えて実際にモデルを使ってみます。以下の例では additionモデルを使って5+3の結果を出力しています。

sess = tf.Session()
output = sess.run(addition, feed_dict = {
  x: 5.,
  y: 3.
})
print(output) # 結果は8.0

　sess.run() にて 実際に計算に使用するモデルを定義し、その際に入力値を与えています。この時点でも、上記計算に「学習」という意味合いは存在しておらず、ただ単純にモデルとデータを元に計算を実行しただけであることに注意してください。

学習

　ただ計算を実行するだけだと味気ないので、今度は学習を行ってみましょう。先ほどadditionモデルを「二つの数の和を計算するモデル」として定義しましたが、今回はこのモデルにちょっと変更を加えて「入力xと変数yを足し算する」というようにしてみましょう。

# -*- coding: utf-8 -*-
import tensorflow as tf

x = tf.placeholder(dtype=tf.float32)
y = tf.Variable(tf.constant(1.))
addition = tf.add(x, y)

　最初のadditionモデルと異なる点として、最初のadditionモデルでは モデルを用いて計算する際にxとyの両方を入力していましたが、新しいadditionモデルで入力するのは xだけである点です。yには初期値として1が代入されているので、このadditionモデルは最初の段階で「x + 1.0」を計算するものとなります。x = 5.0 なら additionの出力は6.0、という具合です。

　さて、ここで この新しいadditionモデルを用いて、どんな実数値xを入れても「x + y = 8.0」となるようなモデルを得たいとしましょう。しかし、このモデルにおけるyはそのままだと初期値 1.0 のままなので、x = 7.0の時以外では理想の結果が得られません。理想の結果を得るためには yの値がうまいこと増減しないといけません(例えばx=12なら、12.0 + y = 8.0 を得るために yの値は初期値である1.0よりも小さい方向にずらす必要がある…等といった具合です)。

　この時点で初めて「学習」という概念を導入します。…とすると、additionはここで初めて「学習前のモデル」という形で認識できます。では y の学習はどのようにして行われるのでしょうか？

　ここで「損失」という概念を導入してみましょう。学習中のモデルによって予測値を計算した際、当然本当の値との誤差があります。この誤差が大きければ大きいほど損失も大きく、小さければ小さいほど損失も小さいと考えます。値が正解から離れれば離れる程損失が大きくなっていく…という仕組みを定量化するために機械学習ではよく二乗誤差を用います。というわけで慣例に従って以下のように損失関数を定義します。

loss = tf.square(tf.subtract(addition, 8))

　学習の目的はこの損失を限りなく少なくしていくことです。ここで損失が限りなく少なくなるということは、予測値が実際の値に限りなく近づいていくことと考えて下さい( ただし、適切でない損失関数の設定が行われた場合等はこの限りではありません )。

　損失を算出する方法はlossによってうまく定義できたものの、「lossによって算出された損失をもとに yの値を修正する」という仕組みが無ければ学習が行えません。幸い、TensorFlowでは予めデフォルトでこの機能を提供してくれます。それが以下のコードにて示す GradientDescentOptimizer という機構です。

optimizer = tf.train.GradientDescentOptimizer(0.2)
train_step = optimizer.minimize( loss )

　GradientDescentOptimizerの引数にある 0.2 というのは学習率のことで、イメージとしては損失関数からの情報を一回の学習でどれだけ参考にして取り入れるかを示すものです( 学習率が高すぎると予測値が振動・発散してしまうリスクが高くなるし、低すぎるといつまでも予測値が正解に近づかないため、状況に応じて適切な学習率の設定が必要です。ただこの辺りの議論に関しては本題の範疇を超えてしまうためここまでにしておきます )。

　ここで、前述の「モデル」の項にて説明した通り、この時点でのtrain_stepはグラフ構造として定義されているだけで、まだ実際の入力値を与えられてもいないし、学習自体も行われていないことを思い出して下さい。実際に計算をする場合は以下のようにします。

sess = tf.Session()
sess.run( tf.global_variables_initializer() ) # 変数の初期化

output = sess.run(train_step, feed_dict = { x: 5.  }) # モデルの学習を行う
y_val = sess.run(y, feed_dict = {x: 5. }) # 学習済のモデルを使って y の値を計算
print("y = %f" % ( y_val )) # y = 1.800000

　x = 5.0 の場合、 y = 3.0 が正解となりますが、train_stepにより一回学習を回してみた所、yは初期値の 1.0 から 1.8 となり、確かに正解に近づいていることが分かります。
　ところで、基本的に学習は複数回数行うものなので、前の例では単純化のためtrain_stepを一回だけ実行するような形にしていましたが、以下のコードのような形に修正して 30回程train_stepによるイテレーションを回してみることにします。この時、yの値はどのように遷移するか見てみましょう。

sess = tf.Session()
sess.run( tf.global_variables_initializer() ) # 変数の初期化

for i in range(30):
  output = sess.run(train_step, feed_dict = { x: 5.  })
  y_val = sess.run(y, feed_dict = {x: 5. })
  addition_val = sess.run(addition, feed_dict = {x: 5. })
  print("5.0 + %f = %f" % ( y_val, addition_val ))

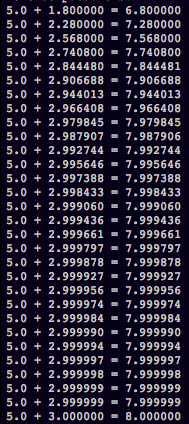
　このコードを実行した結果は以下のようになります。

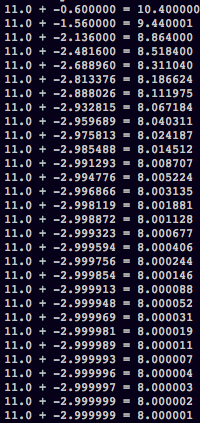
　学習を重ねるにつれて確かにyの値が 3.0 に近づいていることが確認できます。では今度は入力値を変えてみて、 x=11 とした場合どうなるでしょう。

　x=11にしても、ごく僅かな誤差はあるもののほぼ正解に近い値になっています。これがTensorFlowによる学習です。

データセット

　今回の学習モデルでは簡単のため 入力値・正解をただ一つだけ設けましたが、実際にTensorFlowで学習を行う際には 一般的にまとまった複数の入力値・正解のセットをモデルに与えて学習させていきます。
　実際のデータセットを扱う上で重要な観点の一つが、一つのデータセットを「学習用データ」「テスト用データ」の二つのデータ群に分離することです。これは、学習させたモデルで実際でどれくらいの精度が出るのかを確かめるためのデータが必要となるからです。
　一つのデータセットを学習用データ群・テスト用データ群に分ける上で手動でプログラムを構築する必要はなく、scikit-learnがこれに相当する機能を提供してくれているので、こうしたものを使用するのが懸命です。

from sklearn.cross_validation import train_test_split

:
x_train, x_test, y_train, y_test = train_test_split(dataset_x, dataset_y, test_size=0.2, random_state=42)
:

ここで、dataset_x, dataset_y はそれぞれ 入力データ群、入力データに対する正解の群を表しています。

まとめ

　というわけで、一つの塊として見ると膨大で複雑なTensorFlowのコードですが、一つ一つ丁寧に要素を分解して見ていくと意外とそこまで複雑ではありません。ここで説明した概念は単純な多層パーセプトロンに止まらず再帰ニューラルネット等様々なモデルにも適用可能な基礎となるものなので、ぜひ抑えておきたい所です。