Kerasで多層パーセプトロンのモデル構築する際のイメージ(数式無し)
2017.7.27
最近Kerasに関して勉強をする機会があったためまとめました。
Kerasで多層パーセプトロンを構築されている方は 幾何的な理解の助けにご利用下さい。
( どちらかというと学習メモ用に走り書きしただけなので 難解な部分, 認識の誤り等残っている可能性があります。
その際にはお手数ですがTwitter(@irration)までご連絡いただけましたら幸いです )
また、今回はモデル構築部の幾何的な理解を目標としているため、実際のKeras部分を用いた学習に関しては省略しております。ご了承下さい。
通常の多層パーセプトロンの場合
# -*- coding: utf-8 -*- from keras.models import Sequential from keras.layers import Dense, Activation from keras.optimizers import SGD
何はともあれインポート。これらのインポートしたものがそれぞれどういう意味を持つのかは後述します。
num_input_layer = 3 # 入力層のニューロンの数 num_hidden_layer = 4 # 隠れ層のニューロンの数 num_output_layer = 3 # 出力層のニューロンの数
入力層、隠れ層、出力層のニューロンの数を変数として持たせておきます。
model = Sequential()
Sequentialインスタンスを作成しました。
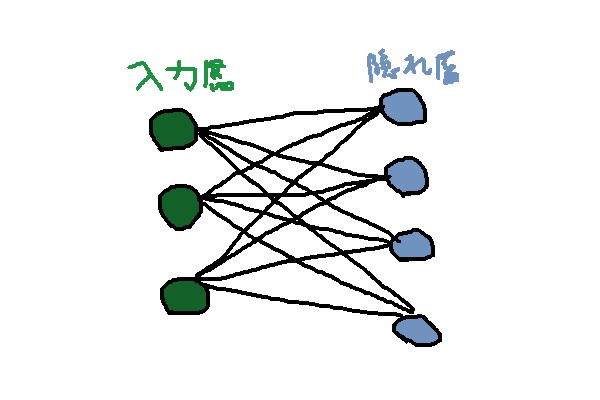
このSequentialというやつは、以下の画像のような複数の層を持つデータをモデル化するためのインスタンスです。
ネットワークの左側の緑色は「入力層」、右側の緑色が「出力層」、(存在する場合)入力層と出力層の間に挟まれているのが「隠れ層」です。
普通のKerasの用途としては隠れ層を複数導入してディープニューラルネットワークのように使うのが通常かと思われますが、一応モデルとして隠れ層を持たない入力層・出力層だけのネットワークのモデル(図の左側に浮いているやつ)も定義できるっぽいです。
というわけで、インスタンスを定義したので早速ですが多層パーセプトロンをつくってみます。
model.add(Dense(num_hidden_layer, input_dim=num_input_layer))
DenseというのはDensely-Connected なニューラルネットの層を指す。
Densely-Connected の イメージとしては上図のようにそれぞれの層の入力と出力同士が全て互いにくっついている感じ。認識が間違っていなければ Fully-Connectedと同義のはず。
( 一応確かめました: dense-vs-convolutional-vs-fully-connected-layers )
今回は入力層が3つ、隠れ層が4つのニューロンからなるため上記のコードにより以下のような図のネットワークができたことになります。
( 因みに この時点で定義されているネットワークにおいて、下記にて隠れ層として描かれているものは モデル上では隠れ層でなく出力層となっています )
次は活性化関数を追加します。活性化関数というのは、あるニューロンが複数の(各ニューロンごとに重みがついた)ニューロンからの入力を受け取り、受け取った値を合計した後 そのニューロン自身を0~1の間の値に落とし込むための関数です。これは連続値の場合もありますし、離散値(0,1)の場合もあります。離散値の場合は「ステップ関数」と言われており、ニューロンが「発火」= 他のニューロンからの入力の合計が閾値を上回りステップ関数が1になる というイメージのものです。活性化関数に関する具体的な議論に関しては他の方の記事に譲ります。
model.add(Activation('sigmoid'))
今回は活性化関数によく使われるシグモイド関数という関数を使用しました。
( なお、最近だとReLU関数というのが使われるのが割とメジャーな方法になってきているっぽいですね )
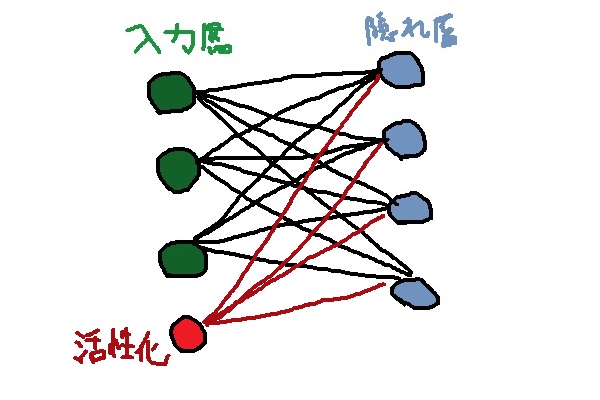
これにより、ネットワークは以下のような状態になりました。
今回は多層パーセプトロンを組みたいので、隠れ層の次に出力層を追加します。
model.add(Dense(num_output_layer))
model.add(Activation('softmax'))
出力層の活性化関数には「ソフトマックス関数」を使用します。ソフトマックス関数は多クラス分類問題においてよく使われる関数で、「これが一番大きい!」と最大の1つを決定する挙動をより緩やかにして、「これが全体の中で結構大きいよね。5つのアウトプットを相対的に表現すると ( 0, 0, 0.03, 0.94, 0.03 ) くらいかな。といった形で「マックス」を「ソフト」にする効用があるため「ソフトマックス」と呼ばれています。
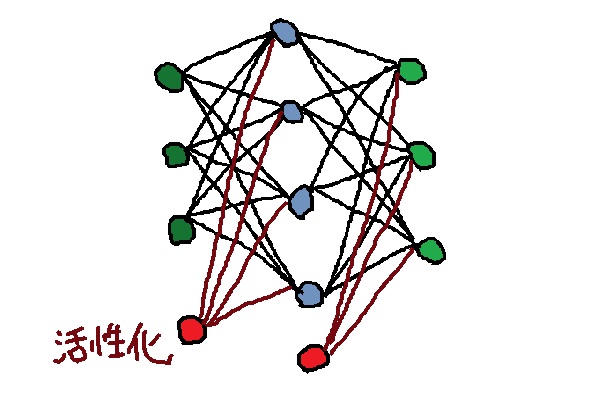
上記コードの追加により、最終的にこんな感じのネットワーク構造ができました。
最後にこのネットワーク構造をコンパイルします。
model.compile(loss='categorical_crossentropy', optimizer=SGD(lr=0.01),metrics=['accuracy'])
( このあたりのコードは後述の書籍(『詳解ディープラーニング』)を参考にさせていただいております。 )
コンパイル時に、どのようにネットワークの学習に際して必要となる情報を併せて引数として渡します。
loss は誤差関数です。テスト時に予測が実際の結果とどれくらいずれていたかをはかる指標です。
【発展的な議論】
因みに誤差関数は何でも良いというわけではなく、活性化関数と対応させる必要があります。
例えば多クラス分類問題を解く際にはソフトマックス関数を活性化関数として選びますが、この場合多クラス用のクロスエントロピー誤差関数を選ぶのが一般的です。
( その他 最小二乗法を用いた回帰問題であれば二乗誤差関数、2クラス分類ならクロスエントロピー誤差関数等 )
optimizerというのは学習の際どのように精度を高めていくかを表す関数です。今回はSGD(Stochastic Gradient Descent; 確率的勾配降下法)という最適化問題における有名な手法を使用します。またこの際lrという引数をSGDに渡していますが、これはlearning rate、すなわち学習率を表し、学習率が大きいほど 誤差をより大きく修正しようという方向で動きます。
metricsはモデルの評価指標です。Kerasではmetrics=['accuracy']という形で設定して、訓練時・テスト時にモデル精度の高さを測る方法がよく使われるようです。
まとめると、以下のようになります。
# -*- coding: utf-8 -*-
from keras.models import Sequential
from keras.layers import Dense
from keras.optimizers import SGD
num_input_layer = 3 # 入力層のニューロンの数
num_hidden_layer = 4 # 隠れ層のニューロンの数
num_output_layer = 3 # 出力層のニューロンの数
model = Sequential()
model.add(Dense(num_hidden_layer, input_dim=num_input_layer))
model.add(Activation('sigmoid'))
model.add(Dense(num_output_layer))
model.add(Activation('softmax'))
model.compile(loss='categorical_crossentropy', optimizer=SGD(lr=0.01),metrics=['accuracy'])
隠れ層を増やしてみる
上記コードの入力層と出力層との間に同じ手順でもう一つ追加するだけです。
model.add(Dense(num_hidden_layer))
model.add(Activation('sigmoid'))
なお、今回は 隠れ層に含まれるニューロンの数をいずれも num_hidden_layer で固定していますが、隠れ層の各層によってニューロンの数を変化させても問題ありません。
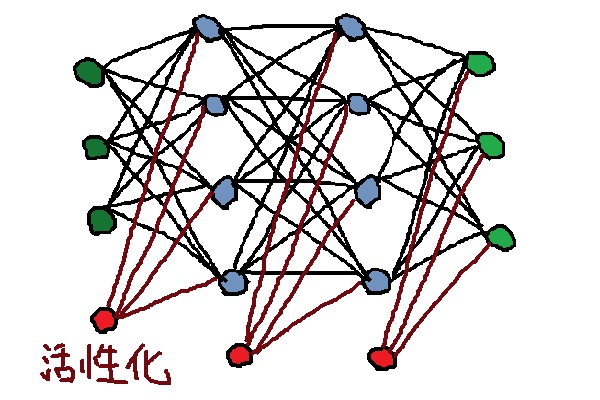
結果的にどういうネットワーク構造になるかというと…
こんな感じです。
コードをまとめると、
# -*- coding: utf-8 -*-
from keras.models import Sequential
from keras.layers import Dense
from keras.optimizers import SGD
num_input_layer = 3 # 入力層のニューロンの数
num_hidden_layer = 4 # 隠れ層のニューロンの数
num_output_layer = 3 # 出力層のニューロンの数
model = Sequential()
model.add(Dense(num_hidden_layer, input_dim=num_input_layer))
model.add(Activation('sigmoid'))
model.add(Dense(num_hidden_layer))
model.add(Activation('sigmoid'))
model.add(Dense(num_output_layer))
model.add(Activation('softmax'))
model.compile(loss='categorical_crossentropy', optimizer=SGD(lr=0.01),metrics=['accuracy'])
となります。Keras、ちょっと触っただけだけど、割と直感的に書けていいな~と思いました。
※ 一部コードは以下の書籍を参考にさせていただいております。RNN, LSTM, BRNN, seq2seq 等の話題も豊富で、且つコードの例も豊富に載っているためオススメです。
Written by Nisei Kimura ( 木村 仁星 )